Efekt piroelektryczny polega na pojawieniu się polaryzacji elektrycznej w wyniku zmiany temperatury kryształu. Dlaczego efekt piroelektryczny występuje w kryształach turmalinu o symetrii punktowej 3m a nie występuje w kryształach kwarcu o symetrii kryształów 32?

Scharakteryzuj w pełni element symetrii generowany przez przekształcenie opisane pozycją równoważną: (-z+1/2, -x+2, y-1/2).

Andrzej Olczak

Jakie pozycje równoważne generuje element symetrii zaznaczony na poniższym rysunku?

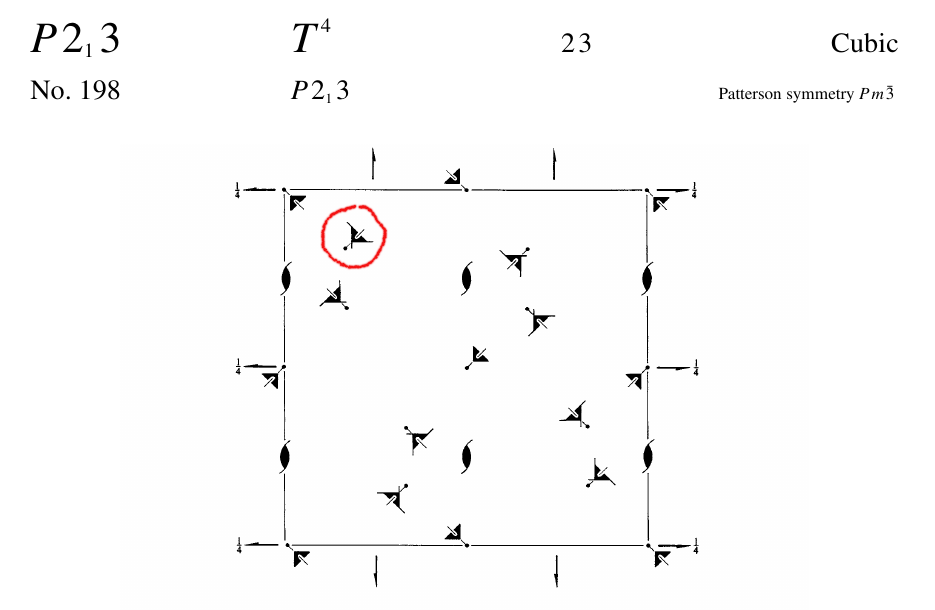
A. Olczak

Mamy dwa kody symetrii opisujące operacje obrotu śrubowego w układzie heksagonalnym:
(-y, x-y, z+1/3) oraz (-x+y, -x, z+1/3). Który z kodów odpowiada osi 3₁ a który 3₂? Jak to rozstrzygnąć?

W układzie heksagonalnym dwukrotna oś śrubowa przebiega równolegle do kierunku [210]. Jej położenie wyznaczone jest przez wektor prostopadły do tej osi i równy -1/4 b + 1/4 c (co oznacza, że nie przechodzi ona przez początek układu współrzędnych, ale przechodzi przez punkt o współrzędnych 0,-1/4,1/4). Jakie będą współrzędne punktu P’ otrzymanego z punktu P o współrzędnych x,y,z po dokonaniu opisanego obrotu śrubowego?

A. Olczak

Pewna operacja symetrii opisana jest kodem (y, -x+y, 1-z). Na podstawie analizy śladu i wyznacznika macierzy tej operacji można zorientować się, że odpowiada to działaniu trójkrotnej osi inwersyjnej. Jak wyznaczyć kierunek tej osi?

J.Chojnacki

W pewnej sieci o prymitywnej komórce elementarnej końce trzech wektorów sieciowych [3-11], [10-2] oraz [-2-11] wyznaczają pewną płaszczyznę sieciową.
Jakie są wskaźniki Millera (hkl) tej płaszczyzny? Ile płaszczyzn sieciowych z rodziny płaszczyzn o tych wskaźnikach leży między zadaną płaszczyzną a początkiem układu współrzędnych?

A. Olczak

Na kryształ dwuwymiarowy o symetrii układu kwadratowego i stałej sieciowej a pada prostopadle do płaszczyzny kryształu promieniowanie rentgenowskie o długości fali λ = 0,5 a. Refleksy o jakich wskaźnikach hk zostaną zarejestrowane na nieskończenie dużym płaskim detektorze ustawionym prostopadle do padającej wiązki promieniowania?

Andrzej Olczak

Ile płaszczyzn sieciowych o indeksach (hkl) przecina prymitywną komórke elementarną?

A. Olczak

Jaką operację symetrii opisuje pozycja równoważna (3/4-x, 1/4+z, 3/4+y)?

A. Olczak