Pytanie nawiązuje do zagadki nr 4.
Czy dla kryształu dwuwymiarowego – jeśli przyjąć, że odległości między liniami sieciowymi
potraktujemy jako odległości międzpłaszczyznowe – obowiązuje prawo Bragga? Może ma jakąś zmodyfikowaną postać, jeśli w ogóle ma?
A. Olczak
Jeżeli przez prawo Bragga (w jakiejkolwiek postaci) rozumiemy jednoznaczną zależność między odległością międzypłaszczyznową, a kątem rozproszenia promieniowania, to odpowiedź na tak ogólnie postawione pytanie brzmi: nie, nie istnieje prawo Bragga (w żadnej postaci) dla kryształów dwuwymiarowych. Wynika to bezpośrednio z konstrucji Ewalda dla kryształów dwuwymiarowych przedstawionej w odpowiedzi na zagadkę nr 4. Widać z niej, że zmieniając orientację kryształu możemy uzyskać promień dyfrakcyjny związany z określonym węzłem sieci o indeksach hk pod różnymi kątami.
To powiedziawszy, można się jednak zastanowić nad postacią takiego prawa dla określonej orientacji kryształu np. ustawionego prostopadle bądź równolegle do padającej wiązki.
Jeżeli prawo Bragga wymaga, aby kąt padania równał się kątowi odbicia, to nie powinno być żadnej dyfrakcji od sieci dwuwymiarowej (np. tkaniny) jeśli źródło promieniowania (laser) ustawiony jest prostopadle do niej. Doświadczenie temu przeczy. Można co prawda kąt ugięcia 2theta obliczyć w przybliżeniu z wzoru Bragga dla niewielkich kątów (wówczas cos(θ) jest prawie jeden), ale generalnie geometria dyfrakcji wymusza stosowanie wzorów Lauego. Poza tym generowane są również refleksy wsteczne, z czego należy sobie zdawać sprawę. Problem ilustrują rysunki poniżej (zrobione dla przestrzeni rzeczywistej). Należy pamiętać, że sin(x) = sin(180-x) i mamy “refleksy wsteczne”.
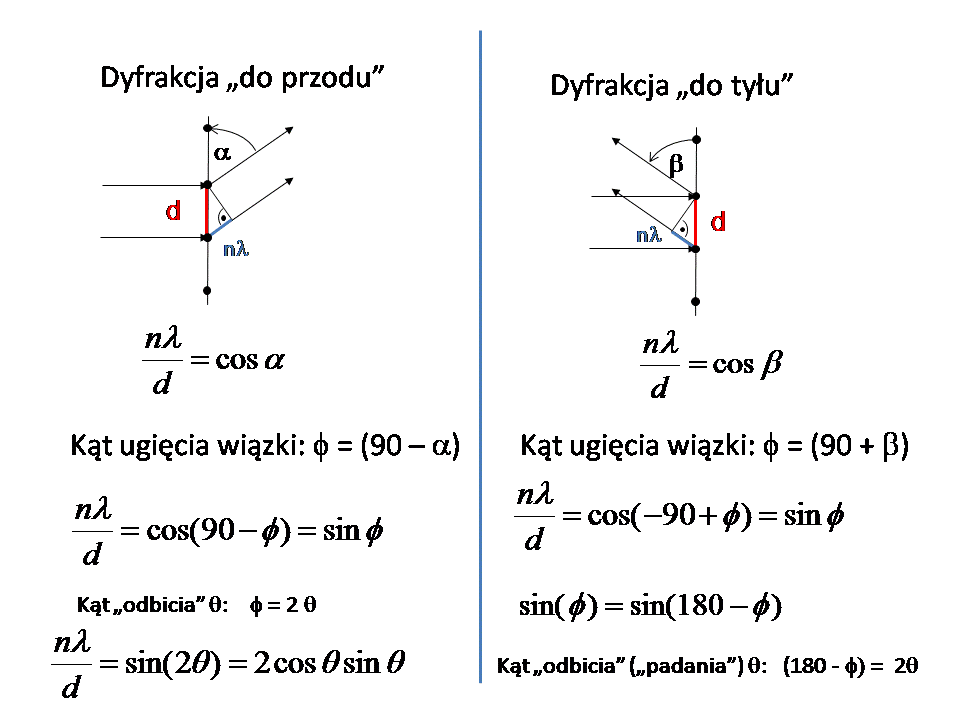
Przedstawione wyprowadzenie w zasadzie dotyczy przypadku jednowymiarowego, ale w przypadku dwuwymiarowego kryształu umieszczonego prostopadle do wiązki padającej równanie jest dokładnie takie samo.
Na poniższym rysunku (zobacz dokładniej jako pdf) przedstawione jest skrótowe wyprowadzenie oparte na konstrukcji Ewalda w 2D. Szczegóły tej konstrukcji zostały opisane w odpowiedzi na zagadkę nr 4 (2 czerwca 2014 o 21:40 ). Kryształ umieszczony jest prostopadle do kierunku wiązki padającej (s0). Na rysunku wybrano przykładowy punkt sieci odwrotnej o współrzędnych (-1,3), z którego wystawiono linię prostopadłą przecinającą sferę Ewalda w punktach A i B. Punkty te wyznaczają kierunki promieni dyfrakcyjnych (s). W rezultacie otrzymujemy równanie: λ= d sin(2θ).
Oczywiście dla innej orientacji kryształu równanie to wyglądałoby zupełnie inaczej. Gdyby np. kryształ był umieszczony równolegle do padającej wiązki (wektory s0 i a* leżą na jednej prostej i mają zgodne zwroty, a wektor b* jest skierowany “do góry”), to równanie to miałoby postać:
λ = -2 sin2(θ) / (ha* + kb*cos(γ*)),
gdzie γ* jest kątem między wektorami sieci odwrotnej a* i b*.
Może dla celów dydaktycznych przypomnę dlaczego konstrukcja Ewalda działa. W pewnym uproszczeniu można powiedzieć, że jeżeli falę płaską opiszemy równaniem typu Asin(2πsr+B), to warunek konstruktywnej interferencji fal Asin(2πs0r+B)) i Asin(2πs1r+B) na węźle położonym w r wymaga, aby Δsr = n (n – liczba całkowita). Wówczas różnica faz wynosi zero lub wielokrotność 2π. Rozpraszanie fali będzie zachodziło dla takich r, które są wektorami sieciowymi (baza abc, współrzędne całkowite) a s jest wektorem falowym, o kierunku zgodnym z rozchodzeniem się fali. Wektor s jest rozpięty na bazie a*, b*, c* wersorów sieci odwrotnej, spełniających a*a=1, b*b=1, c*c=1 a iloczyny mieszane równe zero (np a*b=a*c=0). Jeśli wektor sieci odwrotnej s będzie miał współrzędne całkowite, to zawsze iloczyn skalarny, sr = n, będzie liczbą całkowitą.
Uwaga. Podręczniki fizyki częściej używają równań typu Asin(sr+B) i wówczas warunki sieci odwrotnej ulegają niewielkiej modyfikacji: a*a=2π, b*b=2π, c*c=2π itd. Nie zmienia to istoty sprawy, bo albo 2π pojawia się w równaniu fali, albo mnożymy przez nie wektory sieci odwrotnej.
Dodatkowo zakładamy, że rozpraszanie jest sprężyste i nie ma strat energii, co oznacza, że długość początkowego wektora falowego s0 i długość wektora falowego wiązki rozproszonej s1 muszą być sobie równe. Tę równość zapewnia właśnie sfera Ewalda. Na rysunku z konstrukcją Ewalda umieszczamy tylko wektory z przestrzeni odwrotnej (w jednostkach [1/m], bo jednostką r jest metr).

Poniżej przedstawiłem konstrukcje Ewalda dla sieci 1D w przypadku gdy wiązka pada prostopadle do “kryształu 1D”.
Jak widać nie ma tutaj możliwości aby oprócz węzła (0) inne węzły sieci odwrotnej przechodziły przez sferę Ewalda (przy zachowaniu prostopadłości), ale to nie przeszkadza, aby iloczyn skalarny (s1 – s0)a był liczbą całkowitą. To właśnie jest warunkiem konstruktywnej interferencji. Warunek zgodności faz spełniają wszystkie wektory Δs zaczepione w zerze sieci odwrotnej i o końcu w płaszczyźnie prostopadłej do a* (wektory które rzutowane na a*, dają długość a*). Czyli, jak podał A. Olczak, Δs|| = a*. Warunek zgodności faz spełniają więc wszystkie wektory s kończące się na linii prostej, zawierającej węzeł a* = 1, a warunek sprężystego rozproszenia (w pokazanej płaszczyźnie) tylko dwa wektory s1 i s2, umieszczone na rysunku.
Kolejny rysunek przedstawia konstrukcję i wzory dla wiązki położonej pod kątem alfa do normalnej do sieci. Jak można się przekonać, oba kąty ugięcia dla tej samej płaszczyzny odwrotnej odpowiadającej punktowi (1) sieci odwrotnej, nie tylko nie spełniają prawa Braga, ale też nie mają się do siebie jak x do 180°-x.
Tak więc dla ukośnie położonego kryształu mamy równanie:
sin(α + φ1) = nλ/a + sin(α)
φ2 = 180-φ1 – 2 α
Oczywiście dla α = 0 wzór ten przechodzi w poprzednio wyprowadzony.
Dodam jeszcze kilka uwag natury ogólnej.
Prezentacja warunków Lauego w wielu podręcznikach krystalografii pozostawia duży niedosyt.
1) Nie zwraca się, na ogół, uwagi na to, że podejście Lauego do dyfrakcji promieniowania rentgenowskiego na krysztale jest znacznie bardziej fundamentalne niż podejście Bragga. Widać to choćby w powyższych rozważaniach dotyczących rozpraszania na kryształach dwu- i jednowymiarowych. Prawo Bragga jest tylko konsekwencją warunków Lauego dla kryształów 3D.
2) Bardzo rzadko w podręcznikach do krystalografii prezentuje się trzy (skalarne) warunki Lauego (Δs·a=h, Δs·b=k, Δs·c=l) w postaci jednego równania wektorowego. Można bez żadnej przesady powiedzieć, że to równie (Δs=H, gdzie H jest wektorem sieci odwrotnej) jest kwintesencją dyfrakcji promieniowania X na krysztale 3D.
3) Przy takim podejściu konstrukcja Ewalda (pojawiająca się w wielu podręcznikach jak deus ex machina) staje się oczywistą geometryczną ilustracją tego warunku.
Ja bym jednak nie lekceważył warunku na rozpraszanie sprężyste, co jest dziełem Ewalda. Do warunku Lauego dochodzi więc jeszcze warunek, że bierzemy tylko Δs = s1 – s0, w których długości s1 i s0 są równe.
Ale przecież nie da się wyprowadzić warunków Lauego bez założenia o sprężystości rozpraszania. To założenie leży u podstaw tego wyprowadzenia, więc konstrukcja Ewalda nie wnosi tu nic nowego. Mówiąc inaczej warunek Lauego należy odczytywać jako równanie Δs=H przy założeniu, że s0=s1 (w sensie długości wektorów).
To tak jak z warunkiem dyfrakcjii Bragga: składa się on z równania 2dsin(θ)=λ i dodatkowych informacji o równości kata padania i odbicia oraz o tym, że promień padający, promień odbity i normalna do płaszczyzny odbicia leżą w jednej płaszczyźnie.
Rzeczywiście, warunek stałości długości s oznacza de facto, że mamy zawsze jedną długość fali λ. Zmiana długości wektora falowego, a więc i energii (E=hc/λ), oznacza utratę monochromatyczności i cała konstrukcja się załamuje.
Dodam tylko jeszcze, że warunek dyfrakcji bywa zapisywany inaczej jako 2s0H = H2, (C.Kittel, Wstęp do fizyki ciała stałego). Tutaj litery wytłuszczone oznaczają wektory, a bez wytłuszczenia ich długość. Tam też autor stwierdził, że jest to inna postać Prawa Bragga, co chyba powinno być odwrócone. Prawo Bragga to szczególna postać tego warunku.
P.S. Warunek powyższy wynika z równań: Δs = H, czyli s0+H = s1, ponieważ długość s się nie zmienia mamy s12 = (s0+H)2, czyli 2s0H + H2 = 0. Ponieważ w sieci odwrotnej zarówno H jak i –H należą do sieci odwrotnej mamy 2s0H = H2.
Dwie uwagi.
1) Dla kryształów trójwymiarowych warunki dyfrakcji Bragga i Lauego są równoważne, choć z Lauego prościej przejść do Bragga niż odwrotnie.
2) Zastąpienie H przez -H jest niezrozumiałe i niepotrzebne, ponieważ kąt między s0 i H wynosi 90+θ. W związku z tym cosinus tego kąta równa się ujemnemu sinusowi θ: cos(90 + θ) = -sin(θ) i otrzymujemy to, co trzeba.