W teorii grup punktowych funkcjonują dwie konwencje: międzynarodowa (krystalograficzna) i Schoenfliesa, bardziej popularna w chemii kwantowej i spektroskopii. Oznaczenia krystalograficzne bazują na rotacjach oraz rotoinwersjach, czyli złożeniach obrotu z inwersją. Teoria i znakowanie grup Schoefliesa używa operacji obrotu oraz obrotu niewłaściwego, który jest złożeniem obrotu z odbiciem w płaszczyźnie prostopadłej do osi. Oba podejścia są równoważne i zestaw rozważanych operacji symetrii jest taki sam, tylko ta sama operacja (reprezentowana taką samą macierzą) nazywana jest inaczej w obu konwencjach. Osie obrotów niewłaściwych oznacza się S_n (w krystalografi mamy zwykle tylko n = 1, 2, 3, 4 lub 6).
Jak najprościej poradzić sobie z zamianą notacji?
Jakie operacje rotoinwersji kryją się pod oznaczeniami: S₁, S₂, S₃, S₄ i S₆?

Współrzędne Webera w układzie heksagonalnym (w dwu wymiarach).
Współrzędne wektora – nazwijmy go R – można przedstawić (tak jak w każdym innym układzie) jako odpowiednie rzuty równoległe wektora R = x*a₁ + y*a₂ na osie współrzędnych (rys. 1).

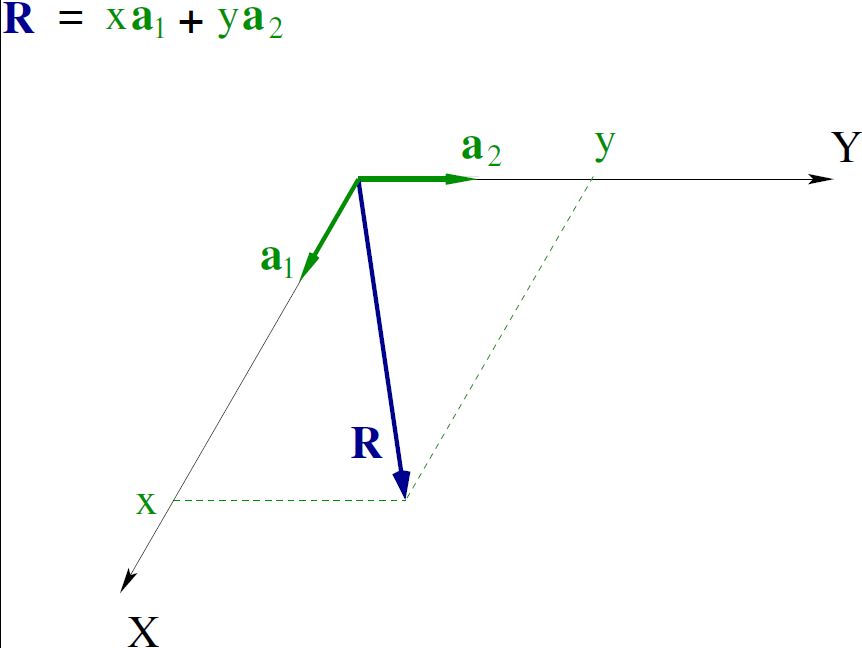
Czasami, ze względu na trójkrotną symetrię występującą w tym układzie, zamiast dwu osi współrzędnych X i Y używa się trzech osi: X, Y, T (rys.2). Są to tzw. współrzędne Webera. W tych współrzędnych wektor R można zapisać jako R = u*a₁ + v*a₂ + t*a₃, a odpowiednie relacje między starymi a nowymi współrzędnymi są następujące: u = (2x – y)/3, v = (2y – x)/3, t = -(x +y). Z powyższych relacji wynika, że u + v + t = 0.

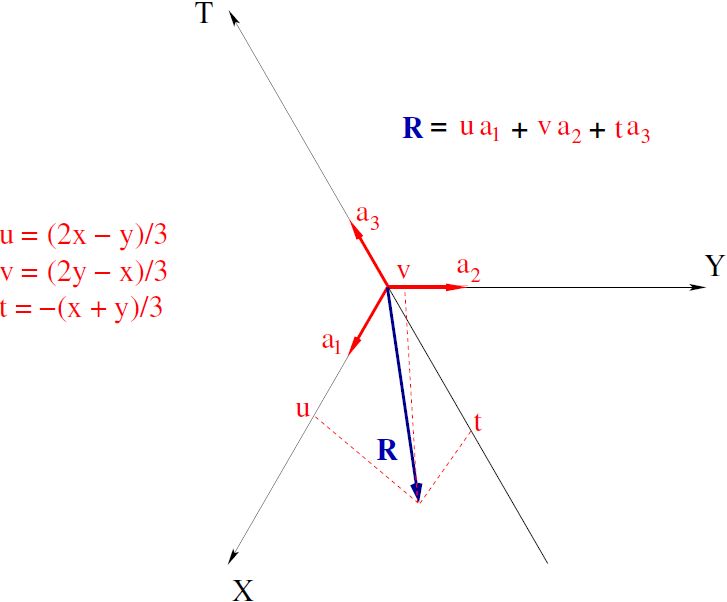
Jaka jest geometryczna interpretacja współrzędnych u, v, t? Nie może być to oczywiście rzutowanie równoległe (do odpowiednich osi współrzędnych) – jak to ma miejsce w przypadku współrzędnych x, y – bo istnieją dwie równoważne osie, wzdłuż których należałoby rzutować, co czyniłoby tę procedurę niejednoznaczną. Może należy wykonać rzutowanie równoległe wzdłuż jakichś innych linii, a może należy rzutować prostopadle do osi współrzędnych?
Andrzej Olczak