Czy poniższa macierz opisuje przekształcenie symetrii ?
|1 1| |0 -1|
A jeśli tak, to jakie i jakim układzie współrzędnych ?
Andrzej Olczak
Czy poniższa macierz opisuje przekształcenie symetrii ?
|1 1| |0 -1|
A jeśli tak, to jakie i jakim układzie współrzędnych ?
Andrzej Olczak
W kartezjańskiej bazie jednostkowej operacja ta nie spełnia warunku dla przekształceń izometrycznych AT = A-1 w wymienionej bazie, a więc nie jest operacją symetrii w tym układzie współrzędnych. Można ją jednak sprowadzić przez podobieństwo do macierzy diagonalnej z 1 i -1 na przekątnej stosując wzór B = QAQ-1, czyli BQ=QA.
Odpowiednie rachunki dają Q (np. można podstawić zmienne a,b,c,d jako elementy tej macierzy i wyznaczyć z układu równań).
Q = |1 1/2| Q-1 = |1 -1/2| |0 1| |0 1|Tak więc operacja ta w układzie współrzędnych z wektorami bazowymi
a1=a i b1=-1/2a+b
będzie operacją izometryczną i będzie to odbicie w osi a1. W nowej bazie współrzędne będą wówczas obliczane jako
x1 = x +1/2y i y1 = y.
Wektory bazowe obliczamy według wzorów macierzowych
Jednak się nie zgodzę z powyższą odpowiedzią. Przedstawiona macierz opisuje odbicie zwierciadlane, którego linia pokrywa się z osią X w układzie współrzędnych, w którym osie X i Y przecinają się pod kątem 60 stopni. Można to łatwo sprawdzić.
Podobnie jest chociażby z macierzą opisującą obrót o 120 stopni w układzie heksagonalnym:
Ewidentnie jest to macierz opisująca przekształcenie symetrii i jednocześnie jest nieortogonalna.
To że macierz nie spełnia warunku ortogonalności, nie oznacza jeszcze, że nie opisuje przekształcenia symetrii, albo inaczej – nie jest izometrią. Aby przekształcenie było izometrią dowolny wektor przed przekształceniem, xi, i po przekształceniu, yi=Sikxk, musi mieć tę samą długość. Można to zapisać jako:
gijxixj = gijyiyj
gdzie – zgodnie z konwencją Einsteina – po powtarzających się wskaźnikach występuje sumowanie.
Prowadzi to do równania macierzowego:
STGS = G
gdzie G oznacza macierz metryczną, której wyrazami są gij.
Powyższe równanie stanowi warunek izometryczności przekształcenia. Oczywiście w przypadku wyboru bazy ortonormalnej (jednostkowej) G staje się macierzą jednostkową a S staje się macierzą ortogonalną.
Podsumowując: o tym czy dana macierz opisuje operację symetrii decyduje nie tylko jej postać, ale również układ współrzędnych, w którym dokonujemy opisu. Ta sama macierz w jednym układzie może opisywać przekształcenie symetrii a w innym -nie.
Po przemyśleniu zgadzam się z opinią, że moja odpowiedź była błędna. Mój bład polegał na zamianie macierzy transformacji. Proszę spojrzeć na załączony rysunek
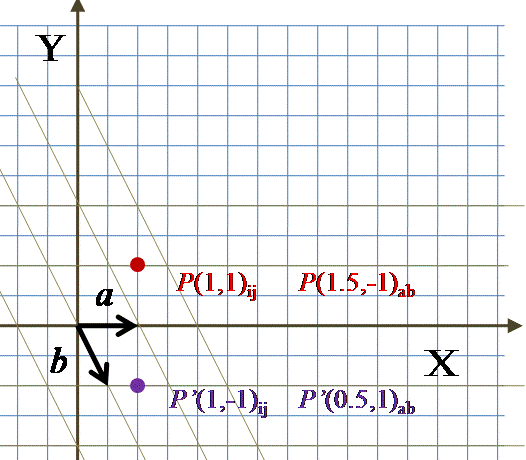 .
.
W układzie ortogonalnym mamy przekształcenie x’ = x, y’ = -y
czyli P(1,1)ij przechodzi w P'(1,-1)ij.
Po przejsciu do nowej bazy punkt P(1.5,-1)ab przechodzi w P'(0.5,1)ab po przemnożeniu przez zadaną macierz
A = 1 1 0 -1.Wszystko się zgadza.
Wyjściowa macierz A należy do tej samej klasy co macierz obicia D w osi X w jednostkowym układzie kartezjańskim ij.
Po przetransponowaniu do nowej bazy [ab] = [ij]S macierz przekszałcenia zapisana w jednostkowym układzie kartezjańskim jako Y = DX przechodzi w Yab = S-1DSXab. Zadanie wymaga aby S-1DS = A
Mam nadzieję, że teraz wszystko jest jasne. Na wszelki wypadek sprawdźmy warunek ortogonalności ATGA = G .
G = aa ab ba bb gdzie a = [1,0], b = [1/2, 1] co daje G = 1 1/2 1/2 5/4.
Dodam tylko, że nowe wektory bazowe nie leżą dokładnie pod kątem 60°, tak więc poprzednia odpowiedź też nie była precyzyjna.
Właściwie zagadka ma wiele (nieskończenie wiele) rozwiązań.
 .
.
 .
.
Przedstawiona macierz reprezentuje operację symetrii odbicia w osi X w każdym układzie współrzędnych o wektorach bazowych
a = [p, 0] i b = [1/2p, q],
dla dowolnych wartości liczb p i q.
Dodatkowo, po zamianie wektorów bazowych, ta sama macierz będzie reprezentować odbicie w osi Y, biorąc
a = [0, p] i b = [q, 1/2p].
Tak więc mówienie o macierzy jako operacji symetrii bez zdefiniowania wektorów bazowych jest nieprecyzyjne. Co prawda jeżeli wiadomo, że mamy na myśli jednostkowy, prawoskrętny układ kartezjański to wówczas takie przypisanie ma sens.
Proszę spojrzeć na załączone rysunki.
Na rysunku podano przykład dla p = 1 i q = 5.
Można sprawdzić, że P’ = A P.
A poniżej wersja dla odbicia w osi Y dla p = 2 q = 1. Ponownie P’ = A P.